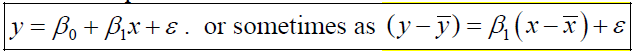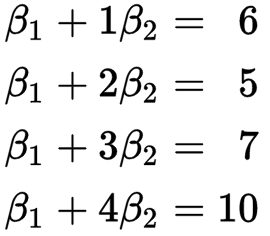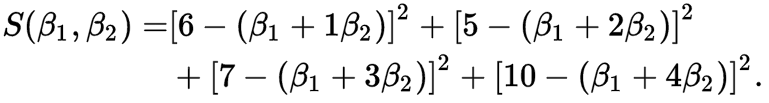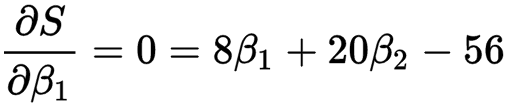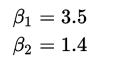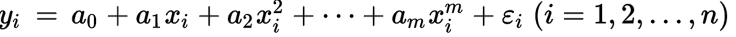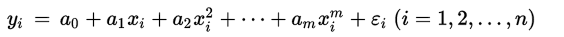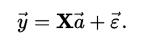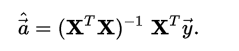Dykin's blog

回归分析是一种很重要的预测建模技术。主要是研究自变量与因变量之间的因果关系。本文将会从数学角度与代码角度分析不同类型的回归。当你想预测连续型的非独立变量，或者对一系列独立变量或输入项有所反应时，就会使用到回归分析。如果非独立变量是二分的，那么我们将会使用到逻辑回归。

对于回归技术的分类，在这里我不想过多细分，但是一般回归会依赖于三个方面进行区分： +自变量数目 +回归函数曲线的形状 +因变量的类型

首先我们来了解下面几种常用的回归算法模型

简单线性回归（Simple Linear Regression）

简单线性回归是最基础的一种回归模型，自变量只有一个，函数曲线为直线，因变量为连续型，自变量可以是连续的或者是离散的。函数表示如下：

其中 y 是因变量， x是自变量， β0 和 β1 属于起始值和系数，ε 为偏移量，为了使得到的函数模型更加准确，最后会加上偏移量。

线性回归一般使用最小二乘法来求解函数模型级求解 β0 和 β1 。方法如下：最小二乘法

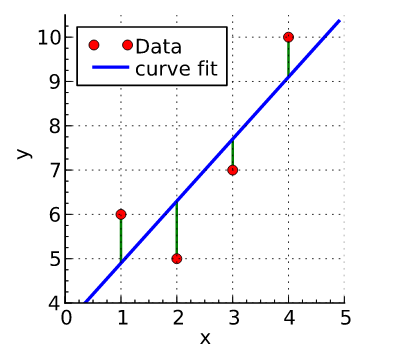
如图中四个点为数据（x,y）:（1,6）（2,5）（3,7）（4,10）。我们需要根据红色的数据来求蓝色的曲线。目前我们已知这四个点匹配直线y= β1 + β2x 。所以我们要找到符合这条直线的最佳情况，即最合适的β0 和 β1。

最小二乘法就是尽量取两边方差的最小值，这样可以找到最拟合的曲线。

然后我们我们同时对β0和β1求其偏导数

这样我们很容易就解除方程组的解

所以我们就得到了直线 y=3.5 + 1.4x

用Python和Java代码表示如下：

# -*- coding: utf-8 -*-
"""
Created on Thu Dec 01 00:02:49 2016

@author: steve
"""

def SLR(x,y):
    intercept = 0.0
    slope = 0.0
    n = len(x)

    sumx = 0.0
    sumy = 0.0
    sumx2 = 0.0

# 第一次循环，得到平均值
    for i in range(n):
        sumx += x[i]
        sumy += y[i]
        sumx2 += x[i]*x[i]

    xbar = sumx/n
    ybar = sumy/n

    xxbar = 0.0
    yybar = 0.0
    xybar = 0.0

# 第二次循环，得到方差
    for i in range(n):
        xxbar += (x[i] - xbar) * (x[i] - xbar);
        yybar += (y[i] - ybar) * (y[i] - ybar);
        xybar += (x[i] - xbar) * (y[i] - ybar);

# 计算斜率和intercept
    slope  = xybar / xxbar
    intercept = ybar - slope * xbar

    print "slope is {}, intercept is {}".format(slope, intercept)
## 其他统计变量我就不写了。

x=[1,2,3,4]
y=[6,5,7,10]
SLR(x,y)

package regression;

public class SLR {

	// 这是用二分法做的简单线性回归

	private final double intercept, slope;
	private final double r2;
	private final double svar0, svar1;

	public SLR(double[] x, double[] y) {

		if (x.length != y.length) {
			throw new IllegalArgumentException("lengths doesn't match!!!");
		}

		int n = x.length;

		// 第一次循环，找到 所有x和y的平均值

		double sumx = 0.0;
		double sumy = 0.0;
		double sumx2 = 0.0;

		for (int i=0; i<n; i++) {
			sumx += x[i];
			sumy += y[i];
			sumx2 += x[i]*x[i];
		}

		double xbar = sumx / n;
		double ybar = sumy / n;

		// 第二次计算，求出方差
        double xxbar = 0.0;
        double yybar = 0.0;
        double xybar = 0.0;
        for (int i = 0; i < n; i++) {
            xxbar += (x[i] - xbar) * (x[i] - xbar);
            yybar += (y[i] - ybar) * (y[i] - ybar);
            xybar += (x[i] - xbar) * (y[i] - ybar);
        }
        System.out.println(xxbar);
        System.out.println(yybar);
        System.out.println(xybar);
        slope  = xybar / xxbar;  //求偏导数的过程
        intercept = ybar - slope * xbar;

        // 其他的统计数据
        double rss = 0.0;      // residual sum of squares
        double ssr = 0.0;      // regression sum of squares
        for (int i = 0; i < n; i++) {
            double fit = slope*x[i] + intercept;
            rss += (fit - y[i]) * (fit - y[i]);
            ssr += (fit - ybar) * (fit - ybar);
        }

        int degreesOfFreedom = n-2;
        r2    = ssr / yybar;
        double svar  = rss / degreesOfFreedom;
        svar1 = svar / xxbar;
        svar0 = svar/n + xbar*xbar*svar1;		

	}

	public double intercept() {
		return intercept;

	}

	public double slope() {
		return slope;

	}

	public double R2() {
		return r2;
	}

	public double slopeStdErr() {
		return Math.sqrt(svar1);
	}

	public double interceptStdErr() {
		return Math.sqrt(svar0);
	}

	//这是预测方法，在机器学习中的函数
	public double predict(double x) {
		return slope*x + intercept;
	}

	public String toString() {
		StringBuilder s = new StringBuilder();
		s.append(String.format("%.2f n + %.2f", slope(), intercept()));
		s.append("  (R^2 = " + String.format("%.3f", R2()) + ")");
		return s.toString();
	}

}

多元线性回归类似于简单线性回归，只不过自变量不止一个，但是过程和方法与简单线性回归一样。这里我只把代码放出来。

多项式回归（Polynomial Regression）

如果一个方程，自变量的指数大于1，那么所有拟合这个方程的点就符合多项式回归。

多项式回归有个很重要的因素就是指数（degree）。如果我们发现数据的分布大致是一条曲线，那么很可能符合多项式回归，但是我们不知道degree是多少。所以我们只能一个个去试，直到找到最拟合分布的degree。这个过程我们可以交给数据科学软件完成。需要注意的是，如果degree选择过大的话可能会导致函数过于拟合，意味着对数据或者函数未来的发展很难预测，也许指向不同的方向。

这个回归的计算需要用到矩阵数据结构。有的编程语言可能需要导入外库。

我们对所有拟合这个公式的点，用矩阵表示他们的关系

如果用矩阵符号表示：

多项式回归向量的系数（使用最小二乘法）：

Java 和 Python 代码如下：

package regression;
import Jama.Matrix;
import Jama.QRDecomposition;

public class PR {

	private final int N;
	private final int degree;
	private final Matrix beta;
	private double SSE;
	private double SST;

	public PR(double[] x, double[] y, int degree) {
		this.degree = degree;
        N = x.length;

        // build Vandermonde matrix
        double[][] vandermonde = new double[N][degree+1];
        for (int i = 0; i < N; i++) {
            for (int j = 0; j <= degree; j++) {
                vandermonde[i][j] = Math.pow(x[i], j);
            }
        }
        Matrix X = new Matrix(vandermonde);

        // 从向量中增加一个矩阵
        Matrix Y = new Matrix(y, N);

        // 找到最小的平方值
        QRDecomposition qr = new QRDecomposition(X);
        beta = qr.solve(Y);


        // 得到y的平均值
        double sum = 0.0;
        for (int i = 0; i < N; i++)
            sum += y[i];
        double mean = sum / N;

        // total variation to be accounted for
        for (int i = 0; i < N; i++) {
            double dev = y[i] - mean;
            SST += dev*dev;
        }

        // variation not accounted for
        Matrix residuals = X.times(beta).minus(Y);
        SSE = residuals.norm2() * residuals.norm2();
	}

	public double beta(int j) {
		return beta.get(j, 0);
	}

	public int degreee() {
		return degree;
	}

	public double R2() {
		return 1.0 - SSE/SST;
	}

	public double predict(double x) {

		double y = 0.0;
		for (int j = degree; j>=0; j--) {
			y = beta(j) + (x*y);
		}
		return y;
	}

	public String toString() {
        String s = "";
        int j = degree;

        // 忽略系数为0.
        while (Math.abs(beta(j)) < 1E-5)
            j--;

        // create remaining terms
        for (j = j; j >= 0; j--) {
            if      (j == 0) s += String.format("%.2f ", beta(j));
            else if (j == 1) s += String.format("%.2f N + ", beta(j));
            else             s += String.format("%.2f N^%d + ", beta(j), j);
        }
        return s + "  (R^2 = " + String.format("%.3f", R2()) + ")";
    }

}

Recent Posts

Links

回归分析总结

-- Nov 18, 2016

简单线性回归（Simple Linear Regression）

多项式回归（Polynomial Regression）

逻辑回归（Logistic Regression）

Probit model

逐步回归（Stepwise Regression）

岭回归（Ridge Regression）

套索回归（Lasso Regression）

弹性网（Elastic net）